esempi di applicazioni dell'analisi matematica

I modelli scientifici non sono veri, ed è proprio questo che li rende utili. Essi
raccontano storie semplici che le nostre menti possono afferrare. Sono bugie
per bambini, storie semplificate per insegnare, e non c'è nulla di male.
Il progresso della scienza consiste nel raccontare bugie sempre più convincenti
a bambini sempre più sofisticati.¹

Di séguito sono riportati alcuni esempi che dovrebbero aiutare il lettore a rispondere alla domanda "a che serve?"

una funzione particolare

Si consideri la funzione y = (x² -1)/ (x + 1).
Abbiamo visto, a proposito del concetto di limite, che la funzione non è definita nel punto x = -1. Questo comporta che possiamo calcolarne il limite, ma non la derivata nel punto x = -1.

Infatti, se scriviamo il rapporto incrementale, otteniamo:

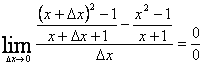
funzione non derivabile in un punto

che porta ad una forma indeterminata 0/0

Le funzioni discontinue non sono derivabili nel punto di discontinuità e, in generale, non sono derivabili funzioni dove c'è un punto angoloso (non esiste la tangente), un flesso a tangente verticale (pendenza infinita) o una cuspide. Questo spiega perché spesso si usa l'intervallo aperto ]a , b[ : serve per precisare che la derivata può essere calcolata solo per valori prossimi quanto si cuole ma diversi da quelli nei punti a e b.

attenzione
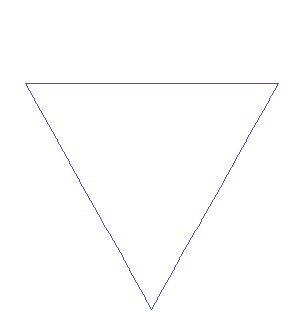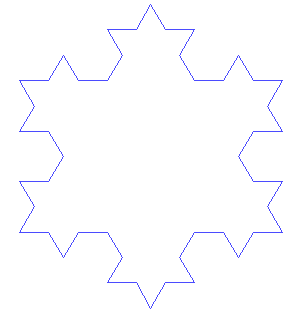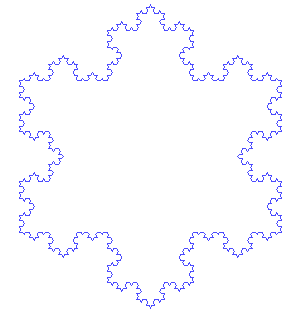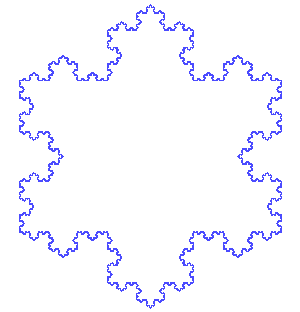
Una funzione può essere continua ma non derivabile; però, se è derivabile è continua. Dunque la derivabilità di una funzione è una condizione sufficiente perché una funzione sia continua; tuttavia, non è una condizione necessaria perché una funzione può essere continua in un punto ma non derivabile in quel punto. Caspita, è complicato, ma l'esempio che segue dovrebbe essere chiarificatore... curva di Koch

Il fiocco di neve di Koch è molto istruttivo per dimostare due importanti osservazioni:

una funzione continua può non essere derivabile in nessun punto (tutti punti angolosi).
un perimetro infinito può contenere un'area limitata;

Per costruire le immagini visualizzate nell'animazione a destra, si parte da un triangolo equilatero e su ogni lato si costruiscono altrettanti triangoli equilateri (poniamo di lato pari a 1/3 del lato di partenza). Poi si fa la stessa cosa su ogni nuovo lato ottenuto e si prosegue per divisioni sempre più piccole, all'infinito, da un punto di vista matematico, oppure fino alle dimensioni di Planck da un punto di vista fisico.

andamento di una funzione

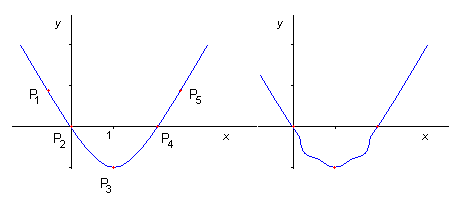nella figura a sinistra è riportato l'andamento della funzione f(x) estrapolato in base a certi punti P_i; a destra è estrapolato un andamento più complesso.

Data una funzione f(x), per tracciarla, si può procedere calcolando il valore assunto dalla funzione in corrispondenza di alcuni valori attribuiti alla variabile x. Ovviamente è necessario un certo criterio per individuare quei punti, x, che possono dare utili informazioni sull'andamento della curva, senza eseguire troppi calcoli aritmetici. Così, per esempio si possono individuare i punti, P, appartenenti alla curva f(x) e supporre che l'andamento sia quello in figura a sinistra. Però, questo procedimento racchiude una certa arbitrarietà: in corrispondenza di P₁, P₂, P₃, P₄, P₅, si potrebbe tracciare anche la curva in figura a destra.

In realtà, per evitare di calcolare un numero elevatissimo di punti, P, si può affrontare il problema con l'ausilio delle derivate, trovando una facile soluzione alla costruzione del grafico: nella figura precedente, corrisponde alla curva a sinistra .
Per esempio, supponiamo di avere la funzione:

y = x² - 2x

la derivata di questa funzione è dy/dx = 2x - 2,

la derivata è nulla per x = 1 mentre è positiva per x > 1 ed è negativa per x < 1

il valore della funzione nel punto x = 1 risulta: y = (1)² - 2 (1) = -1

La funzione incontra l'asse delle x nei punti x = 0 e x = 2 ; è crescente per tutti i valori maggiori di 1 ed è decrescente per tutti i valori minori di 1, deve avere un minimo nel punto x = -1 (derivata nulla); con questi elementi è non ci sono ambiguità nel tracciarne il grafico.

Il pulsante rimanda ad un programma on-line per tracciare il grafico di una funzione:

espansione di un gas ideale

L'osservazione sperimentale ha mostrato che riscaldando un gas in un recipiente munito di un pistone mobile, il volume aumenta e tuttavia la pressione del gas si mantiene costante ed uguale a quella esterna. In questo caso, la variazione di volume è data dall'espressione:

V = V_o (1 + α) t

Viceversa, riscaldando un gas racchiuso in un recipiente chiuso in modo che il volume sia invariabie, la variazione nella pressione del gas è data dall'espressione:

p = p_o (1 + α) t

Se vogliamo calcolare il lavoro necessario per sollevare il pistone mobile che racchiude un gas contenuto in un cilindro, possiamo procedere in questo modo:

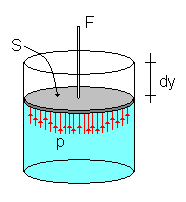lavoro espansione/compressione di un gas la forza F necessaria per sollevare di un tratto dy il pistone è data dal prodotto della pressione, p, applicata per la superficie, S, della parete mobile: F = p · S

il lavoro necessario sarà dunque F · dy = p · S · dy = p · dV dove: S · dy = dV

con questa notazione vogliamo indicare che la pressione applicata, p, può ritenersi costante durante una variazione di volume estremamente piccola (infinitesima). Se poi vogliamo calcolare il lavoro associato ad una variazione di volume finita, cioè conseguente ad una successione di volumi dv estremamente piccoli, occorre un'operazione di integrazione:

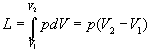
lavoro di un gas

dove si è supposto che la pressione sia mantenuta costante durante tutto il processo.

Però, se la pressione durante l'espansione varia, allora nel caso che la temperatura sia costante durante il processo, per calcolare l'integrale dobbiamo tener conto che p varia con il variare del volume secondo l'equazione di stato dei gas:

p = RT/V

così, il lavoro di espansione diventa:

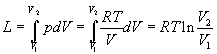
espansione di un gas isotermo

alcune applicazioni alla Geometria

1) superficie del cerchio

Un metodo semplice per calcolare l'area del cerchio consiste nel pensare che la sua superficie sia data dalla somma progressiva di infiniti cerchi concentrici che hanno come valore minimo il centro del cerchio e come massimo il raggio, R, della circonferenza in oggetto. Praticamente, è come se addizionassimo tra loro infiniti anelli, aventi ognuno spessore infinitesimo. Ponendo che ogni singola circonferenza abbia lunghezza π r , otteniamo la funzione che ci dà le diverse circonferenze (separate dal fattore infinitesimo dr). L'integrale tra il valore minimo, 0, e massimo, R, risolve il problema:

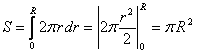
area del cerchio

2) volume della sfera

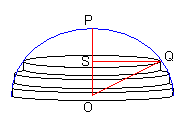per calcolare il volume di una sfera, prendiamo in considerazione una semisfera e immaginiamo che sia riempita con n cilindri sovrapposti, ciascuno di base circolare decrescente. E' intuitivo che se l'altezza di ogni singolo cilindro è infinitesima, la loro sovrapposizione approssimerà molto bene il volume della semisfera.

sia π x² dz il volume di ogni singolo cilindro di raggio x e altezza infinitesima dz.

Il volume della semisfera sarà dato dalla somma integrale di tutti i cilindri sovrapposti:

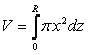(1)

per calcolare questo integrale, occorre considerare che il raggio, x, della base di ogni cilindro diminuisce via via che un cilindro si sovrappone all'altro. Così, dalla figura si vede che OS = z ; OQ = R ; SQ = x e dunque, per il teorema di Pitagora: z² + x² = R². Ricavando x e sostituendolo nell'integrale (1), abbiamo:

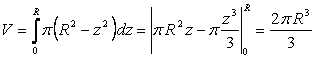
ora, per ottenere il volume della sfera basta moltiplicare per 2 il risultato ottenuto.

3) volume del cono

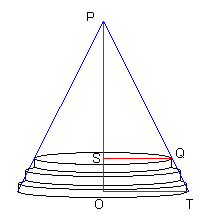
il procedimento è analogo a quello esaminato per calcolare il volume della sfera.

sia π x² dz il volume di ogni singolo cilindro di raggio x e altezza infinitesima dz.

Il volume del cono sarà dato dalla somma integrale di tutti i cilindri sovrapposti:

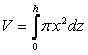(2)

per calcolare questo integrale, occorre considerare che il raggio, x, della base di ogni cilindro diminuisce via via che un cilindro si sovrappone all'altro. Così, dalla figura si vede che SP = z ; SQ = x ; OP = h ; OT = R . Poiché vale la proporzione:

SP : SQ = OP : OT cioè z : x = h : R

Ricavando x e sostituendolo nell'integrale (2), abbiamo:

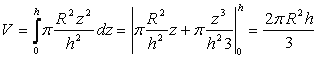
volume del cono

4) superficie della sfera

calcolando la derivata del volume della sfera rispetto al raggio, secondo la definizione si calcola il limite seguente:

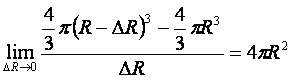
superficie della sfera

Quando ΔR tende a zero, ΔV tende sempre di più al volume di un guscio avente superficie pari a quella della sfera e spessore ΔR. Quindi, dividendo tale volume per lo spessore del guscio, non può che rimanere, sempre al limite, l'area della superficie della sfera.

problemi di massimo e minimo

Come incrementare la produttività delle mucche da latte
L’UPLI – Unione Produttori Latte Italiani, decise di finanziare una ricerca scientifica per aumentare la produttività delle mucche da latte, ovverosia produrre la stessa quantità con meno mucche. Così decisero di chiedere ai migliori biologi e ingegneri genetici di creare una mucca migliore. Gli scienziati richiesero costosi prodotti chimici, strani batteri, moltissime attrezzature da quarantena, e dopo due anni uscirono dai laboratori con la “mucca progredita”. Essa produceva il 2% di latte in più rispetto a una mucca normale. A questo punto l’UPLI si rivolse ai fisici, i quali ricavarono ben poco. Un soggetto sottoposto a radiazioni produsse il 10% di latte in più. Il latte, però, non era a norma di legge e la vita del soggetto era dimezzata. Nella disperazione, l’UPLI affidò l’incarico ad un gruppo di matematici che dopo aver ascoltato il problema chiesero alla delegazione dell’UPLI di ritornare quello stesso giorno, nel tardo pomeriggio. Quando tornarono, ricevettero un foglio di carta nel quale c’erano tutti i calcoli per ottenere la “nuova mucca migliorata del 300%”. Il progetto cominciava così: Una dimostrazione della possibilità di aumentare del 300% la produttività di latte dei bovini. Si consideri una mucca sferica...
(tradotto, con varianti, da Chet Murthy, Cornell)

le questioni di massimo e di minimo hanno sempre avuto un grande valore nell'interpretazione dei fenomeni naturali, sulla scia del principio aristotelico secondo cui la natura sceglie sempre la via più facile... nulla accade nell'universo che non faccia capo a qualche criterio di massimo o di minimo..., così si esprimeva Eulero.

1) In base a dati storici, un certo appezzamento di terreno può essere coltivato a frutteto piantandovi 50 alberi di mele in un frutteto. Ogni albero produce 800 mele. Per ogni ulteriore albero piantato nel frutteto, la produzione per albero si riduce di 10 mele. Quanti alberi dovrebbero essere aggiunti al numero suggerito al fine di massimizzare la produzione totale di alberi?

Indicando la produzione totale con P:

P = (numero di alberi) (produzione di mele per albero)

40000 = (50)(800)

P = (50 + x) (800 - 10x)

dP/dx = 300 - 2x ; questa equazione si annulla per x = 15

in questo modo si ottiene la maggior produzione possibile di mele.

Infatti, con 65 alberi si ottiene P = 65 (800 - 150) = 42250 mele

Con 64 alberi si ottiene P = 64 (800 - 140) = 42240;

con 66 alberi si ottiene P = 66 (800 - 160) = 42240.

2) Un problema interessante è cercare l'altezza, h, di un barattolo di alluminio tale che a parità di volume, V, abbia la minima superficie, S. In questo modo, si contiene il costo di produzione per la parte relativa all'alluminio.

Il volume di un cilindro è : V = 2π R² ; (1)

la superficie del cilindro è : S = 2π R² + 2π R h ; (2)

sostituendo la (1) nella (2), si ottiene:

S = 2π R² + 2π R (V/2π R²) ; (3)

derivando la (3) rispetto al raggio, si ottiene:

dS/dR = - 2π V/R² + 4 π R

annullando la derivata, e con facili passaggi si trova il minimo della funzione, per cui risulta

h = 2 R

la dimensione ottimale di un barattolo comporta che l'altezza sia uguale al diametro della base... non perdete tempo a controlllare sugli scaffali dei supermercati: difficilmente troverete qualche lattina che rispetta le proporzioni ottimali.

biofarmaceutica

3) ci proponiamo di calcolare la concentrazione ematica massima conseguente ad un farmaco assunto per via orale. La formula discussa nella parte di biofarmaceutica è la seguente:

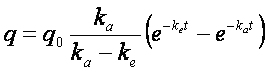(1)

per semplicità, indichiamo le costanti con la lettera A

(2)

la derivata calcolata rispetto al tempo, t, e poi eguagliata a zero (4) per trovare il massimo fornisce:

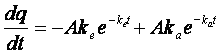(3)

(4)

rislvendo rispetto a t, si ottiene il tempo in cui si raggiunge la concentrazione ematica massima:

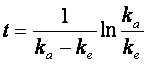
¹Jack Cohen, Terry Pratchett e Ian Stewart, The Science of Discworld II - The Globe, Random House 2003, pag. 248

1	2	3	4	5	6	7	8
HOME PAGE